Exceptional inverse image functor
In mathematics, more specifically sheaf theory, a branch of topology and algebraic geometry, the exceptional inverse image functor is the fourth and most sophisticated in a series of image functors for sheaves. It is needed to express Verdier duality in its most general form.
Definition
| Image functors for sheaves |
|---|
| direct image f∗ |
| inverse image f∗ |
| direct image with compact support f! |
| exceptional inverse image Rf! |
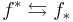 |
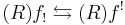 |
Let f: X → Y be a continuous map of topological spaces or a morphism of schemes. Then the exceptional inverse image is a functor
- Rf!: D(Y) → D(X)
where D(–) denotes the derived category of sheaves of abelian groups or modules over a fixed ring.
It is defined to be the right adjoint of the total derived functor Rf! of the direct image with compact support. Its existence follows from certain properties of Rf! and general theorems about existence of adjoint functors, as does the unicity.
The notation Rf! is an abuse of notation insofar as there is in general no functor f! whose derived functor would be Rf!.
Examples and properties
- If f is an immersion of a locally closed subspace, then it is possible to define
-
- f!(F) := f∗ G,
- where the sections of G on some open subset U of Y are the sections s ∈ F(U) whose support is contained in X. The functor f! is left exact, and the above Rf!, whose existence is guaranteed by general structural arguments, is indeed the derived functor of this f!. Moreover f! is right adjoint to f!, too.
- Slightly more generally, a similar statement holds for any quasi-finite morphism such as an étale morphism.
- If f is an open immersion, the exceptional inverse image equals the usual inverse image.
References
- Iversen, Birger (1986), Cohomology of sheaves, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-3-540-16389-3, MR842190 treats the topological setting
- Grothendieck, Alexandre (1977), Séminaire de Géométrie Algébrique du Bois Marie - 1965-66 - Cohomologie l-adique et Fonctions L - (SGA 5), Lecture notes in mathematics, 589, Berlin, New York: Springer-Verlag, pp. xii+484, ISBN 978-3-540-08248-4 treats the case of étale sheaves on schemes. See Exposé XVIII, section 3.